Pourquoi prouver l’intégrité d’un journal de logs ?
Dans la plupart des systèmes modernes, conserver un journal de logs permet de retracer les actions effectuées et de comprendre ce qui s’est passé en cas d’incident. En cybersécurité, on parle souvent d’audit trail.
Le logging est une brique essentielle de tout système qui manipule des données sensibles. Il sert à la fois à diagnostiquer, auditer et répondre aux incidents. Le problème c’est qu’après la base de données, la deuxième cible d’un attaquant est souvent les logs eux-mêmes : en les altérant, il peut dissimuler une compromission ou effacer toute preuve d’accès non autorisé, ce qui rend la détection et la réponse beaucoup plus difficiles.
Si ces journaux peuvent être modifiés ou supprimés, alors toute la chaîne de confiance devient discutable.
Certaines normes exigent d’ailleurs que ces logs soient infalsifiables.
C’est le cas de la
NF525* (certification des logiciels de caisse), mais aussi de la norme
PCI-DSS (sécurité des paiements) ou encore du
HDS pour les hébergeurs de données de santé (calqué sur la norme
ISO 27001).
Même en dehors des contraintes réglementaires, dans des domaines comme la santé ou la finance, la capacité à garantir l’intégrité des logs n’est plus un luxe mais une nécessité.
Lorsqu’on conçoit un tel système, trois aspects méritent une attention particulière :
La complexité d’intégration côté applicatif,
Les coûts induits par le stockage et la signature numérique,
La charge opérationnelle liée à la gestion et à la vérification des logs sécurisés.
Dans ce billet, nous allons comparer deux approches pour atteindre cet objectif :
une implémentation naïve fondée sur une
blockchain (qui est une solution simple et efficace, mais qui ne permet pas le roulement des logs),
une version plus efficace et pragmatique construite autour des
Merkle Trees*.
Nous considérerons ici que nos logs ont la structure simple ci-dessous, mais elle peut être étendue selon les besoins (source, level, …).
type LogEntry struct {
Message string `json:"message"`
Timestamp time.Time `json:"timestamp"`
}
Implémentation naïve : une blockchain
La chaîne de hachage (appelée blockchain par abus de langage), bien que liée surtout à l’univers des cryptomonnaies aujourd’hui, est un concept cryptographique qui remonte aux années 80, et dont le premier cas d’usage concret était l’horodatage de documents numériques afin d’empêcher leur falsification.
Une chaîne de hachage est simplement une liste de blocs de données, où chaque bloc est haché sur la concaténation du checksum du bloc précédent et de ses propres données (SHA-256 ou BLAKE3 par exemple). (en utilisant
SHA-256 ou BLAKE3 par exemple).
Transposée à un journal de logs, cela revient à forger un bloc par entrée ; dès qu’on veut purger, il faudrait rejouer ou re-signer des millions de blocs, ce qui est disproportionné pour un simple journal applicatif.
Étant donné que le premier bloc de la chaîne n’a pas de parent, il est le seul point de confiance de notre système, c’est pour cela qu’il est souvent appelé “bloc 0” ou “bloc genèse” (genesis block en anglais).
Schéma d’implémentation d’une chaîne de hachage
Bien qu’en pratique ce système soit cohérent, il présente plusieurs limites dans la pratique.
Un attaquant peut, en théorie, recalculer l’intégralité de la chaîne s’il a accès au bloc genèse : il suffit de forger un nouveau bloc 0, de rejouer tous les hashes et de remplacer le journal par cette version falsifiée, que la vérification locale acceptera. On ne fait alors que réduire le risque, pas le supprimer, tant que le point d’ancrage reste dans le même périmètre de confiance que les logs. Ce n’est qu’en externalisant ou en signant cryptographiquement la racine (ex. signature avec une clef stockée ailleurs ou publication périodique hors du SI) que l’on rend ce recalcul indétectable impossible
La vérification d’une chaîne de hachage complète reste également linéaire : il faut rejouer chaque bloc pour confirmer l’intégrité de l’ensemble. Sur de gros volumes de logs, cela devient rapidement coûteux en ressources.
Autre problème : l’absence totale de parallélisation. Chaque bloc dépend du précédent, ce qui empêche de recalculer ou de vérifier plusieurs parties de la chaîne en parallèle. C’est un bottleneck majeur pour les applications à fort trafic ou les architectures distribuées.
Enfin, une chaîne de hachage ne permet aucune rotation naturelle des logs : dans un contexte de rétention de plusieurs années (ce qui est plutôt commun dans le cadre de plusieurs normes), il faut supprimer l’intégralité de l’historique, puis reconstruire une nouvelle chaîne à partir de zéro, une opération particulièrement lourde et peu réaliste pour des journaux applicatifs.
Arbre de Merkle : une alternative plus flexible
Une approche plus flexible consiste à remplacer la chaîne de hachage par un arbre de Merkle.
Utilisé dans le système de fichier
ZFS pour contrer la dégradation des données dans un
RAID ou dans des protocoles comme
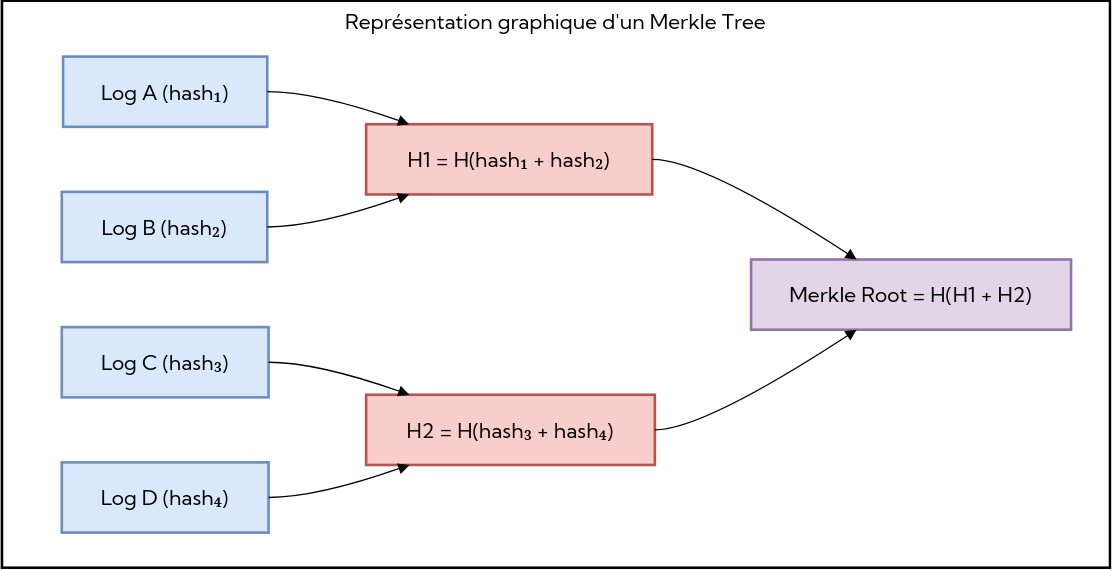
IPFS, le concept des arbres de Merkle est de regrouper les logs sous forme de feuilles dans un arbre binaire. Chaque feuille contient le hash du log, et chaque nœud interne contient le hash de la concaténation de ses deux enfants. Le sommet de l’arbre, appelé “racine” représente un engagement cryptographique sur l’ensemble des logs.
L’intérêt de ce modèle est de permettre une vérification beaucoup plus rapide et partielle. Pour prouver qu’un log donné appartient bien à l’arbre, on fournit :
le hash de la feuille (le log lui‑même),
la liste ordonnée des hashes frères rencontrés en remontant vers la racine, ainsi que leur position gauche/droite.
Le vérificateur recalcule alors, étape par étape, le hash du parent à partir du hash courant et de son frère, puis celui du niveau supérieur, jusqu’à recomposer la racine. Si la racine obtenue correspond à la racine publique, la preuve est acceptée ; sinon elle échoue. Cette preuve, appelée Merkle Proof (ou “preuve d’appartenance”), se calcule en complexité logarithmique.
Cette approche corrige pratiquement tous les inconvénients d’une chaîne de hachage lorsqu’on parle de journaux de logs.
Il n’est plus nécessaire de rejouer l’intégralité de la séquence d’événements, pour vérifier un log il suffit d’une preuve d’appartenance, composée uniquement des hashs latéraux.
Chaque sous-arbre peut être calculé indépendamment, cela permet de distribuer le calcul sur plusieurs machines (ou threads), ce qui élimine le goulot d’étranglement inhérent à la chaîne de hachage (où chaque bloc dépend du précédent).
On peut tronquer ou archiver un sous-arbre complet sans casser la validité du reste : on coupe le lien vers la partie obsolète, on recalcule les hashes jusqu’au nœud de coupe et on considère ce nœud comme nouvelle racine pour la fenêtre courante. Pas besoin de supprimer ni de rejouer toutes les feuilles conservées.
Chaque service ou VM peut construire son propre arbre en parallèle et publier sa racine, ces racines peuvent ensuite être combinées dans un arbre de racines, ce qui rend le modèle parfaitement scalable horizontalement.
Proof of concept
Ce PoC fixe quatre objectifs :
Construire et mettre à jour la racine en streaming via un StreamBuilder, en O(log n) mémoire (il n’y a donc pas d’arbre complet en RAM).
Générer et vérifier des preuves d’inclusion avec un arbre explicite, sérialisable en SQLite pour audit et reconstruction.
Valider l’équivalence stream <=> arbre, y compris en concurrence, via tests déterministes et fuzzing.
Publier régulièrement les racines (et signatures) en stockage immuable type S3 Object Lock / équivalent, pour dater et verrouiller les checkpoints.
Afin de vérifier la théorie, nous avons implémenté un PoC en Go (qui offre des outils de fuzzing natifs à la toolchain Go), qui tient en quelques modules Go simples : une struct LogEntry, des digests avec séparation de domaine, un StreamBuilder en O(log n) mémoire, un arbre explicite pour la génération de preuves et une persistance SQLite pour l’audit.
const (
leafPrefix byte = 0x00
internalPrefix byte = 0x01
)
func LeafDigest(e LogEntry) [32]byte {
m := e.Serialize()
b := make([]byte, 1+len(m))
b[0] = leafPrefix
copy(b[1:], m)
return sha256.Sum256(b)
}
func CombineDigests(l, r [32]byte) [32]byte {
var buf [1 + 32 + 32]byte
buf[0] = internalPrefix
copy(buf[1:33], l[:])
copy(buf[33:], r[:])
return sha256.Sum256(buf[:])
}
Le préfixe 0x00 pour les feuilles et 0x01 pour les nœuds internes évite toute collision structurelle (un message ne peut pas “ressembler” à un nœud).
Arbre explicite et preuves
Node porte soit une feuille (Data), soit des pointeurs Left/Right et un hash mis en cache.
BuildMerkleRoot replie chaque niveau jusqu’à la racine.
GenerateProof remonte de la feuille à la racine en collectant les hashes frères et leur position gauche/droite.
VerifyProof refait le chemin et compare à la racine attendue.
type ProofStep struct{ Hash [32]byte; Right bool }
func VerifyProof(leaf LogEntry, proof []ProofStep, root [32]byte) bool {
h := LeafDigest(leaf)
for _, s := range proof {
if s.Right { h = CombineDigests(h, s.Hash) } else { h = CombineDigests(s.Hash, h) }
}
return h == root
}
Streaming en O(log n)
StreamBuilder accumule un hash “par niveau” (compteur binaire) et ne garde qu’un slot par hauteur d’arbre.
type StreamBuilder struct {
mu sync.Mutex
levels []levelDigest
entryCount int
}
func (s *StreamBuilder) AddEntry(e LogEntry) {
d := LeafDigest(e)
s.mu.Lock()
s.foldDigestLocked(0, d)
s.entryCount++
s.mu.Unlock()
}
func (s *StreamBuilder) Root() ([32]byte, bool) {
s.mu.Lock(); defer s.mu.Unlock()
var out [32]byte; var ok bool
for _, slot := range s.levels {
if !slot.filled { continue }
if !ok { out, ok = slot.hash, true; continue }
out = CombineDigests(slot.hash, out)
}
return out, ok
}
On obtient la même racine qu’avec un arbre complet, mais sans stocker l’arbre.
Persistance et audit
L’arbre peut ensuite être stocké en base de donnée en insérant les feuilles (payload + hash) ainsi que les nœuds internes (niveau, position, hash), ce qui permet :
de rejouer l’arbre / vérifier des preuves localement
d’exporter les feuilles originales pour une fenêtre de N jours en arrière
d’inspecter la structure en triant par level / position.
Tests, robustesse et fuzzing
L’objectif des tests est double : verrouiller les invariants cryptographiques (séparation de domaine, ordre gauche/droite, stabilité) et assurer que le chemin streaming en O(log n) produit exactement la même racine et les mêmes preuves qu’un arbre explicite, y compris en environnement concurrent où plusieurs goroutines alimentent et lisent l’état en parallèle.
Invariants de hash et d’ordre
Séparation de domaine effective : un hash de feuille ne doit jamais égaler un hash interne avec le même payload (préfixes 0x00 / 0x01).
Non-commutativité : inverser gauche/droite doit donner un digest différent, ce qui empêche de réordonner les enfants sans alerter.
Stabilité : à entrée identique, le digest est stable (pas d’état caché ni de source de hasard).
Arbre, preuves et négatifs
Une preuve d’appartenance pour une feuille réelle est valide en recomposant jusqu’à la racine attendue. Les altérations négatives échouent (même preuve mais payload modifié, ou même payload avec permutation d’un hash frère).
Une preuve correcte appliquée à une racine différente doit aussi échouer, ce qui protège contre les relectures hors fenêtre.
Concurrence
Plusieurs goroutines construisent chacune un stream sur le même lot d’entrées et comparent à la racine de référence (testé avec -race).
La génération puis vérification simultanée de proofs sur un arbre partagé valide la lecture thread-safe et la pureté des fonctions sur les hashes. En concaténation progressive, on ajoute des entrées pendant qu’un autre thread lit la racine, sans divergence observable.
Fuzzing
Les fuzzers génèrent des séquences aléatoires de logs, construisent la racine, vérifient une preuve sur un index aléatoire, puis altèrent payload ou ordre des frères pour s’assurer que la preuve échoue.
La parité entre StreamBuilder et BuildMerkleRoot est vérifiée sur des tailles impaires ou des niveaux incomplets pour garantir la même racine.
Des cas bornés (taille 1, 2 et puissances de deux) vérifient le chaînage des slots et les duplications éventuelles de dernière feuille.
Les tests de fuzzing tournent en continu sur une petite fuzzing farm de 56 vCPU pendant l’équivalent de 176 heures de temps CPU (~3h de temps réel) sans faux-négatif, faux-positif, crash ni timeout, ce qui donne une bonne couverture des chemins critiques.
Checkpointing et ancrage immuable pour la conformité
Une fois la racine Merkle calculée, il faut l’ancrer quelque part, c’est-à-dire la publier dans un espace où elle ne pourra plus être modifiée.
Pourquoi ancrer les checkpoints ?
Le Merkle tree nous donne une racine unique qui représente l’état exact des logs à un instant T.
Mais cette racine reste un simple hash : si elle est stockée dans une base de données classique ou sur un disque, rien n’empêche de la réécrire plus tard.
Pour que la preuve reste valable juridiquement et techniquement, il faut que chaque racine soit immutabilisée dès sa publication.
on calcule une racine pour une période donnée (ex. un jour)
on la publie dans un stockage immuable
on ne la touche plus jamais
Ainsi, un auditeur qui vérifie un log à J-45 n’a qu’à comparer la preuve à la racine du checkpoint de J-45 pour s’assurer qu’elle était déjà ancrée à cette date.
À quelle fréquence publier la racine ?
La racine doit couvrir la période du log à vérifier. Si vous ne publiez qu'une racine par jour à 23:59, un log du matin ne pourra être auditable de façon immuable qu'après la publication du checkpoint du soir. Voici deux options en pratique :
Publier plus souvent (ex. toutes les heures, ou toutes les 10k entrées). Le coût est négligeable car un checkpoint n'est qu'un hash + signature.
Conserver une racine "de travail" générée en continu (le StreamBuilder sait donner la racine à tout instant) et l'ancrer dans l'object store dès qu'un audit est demandé. Cette racine instantanée devient alors le point de référence pour ce log.
S3 Object Lock : immutabilité garantie au niveau du stockage
Sur AWS, la solution la plus simple pour obtenir cette immutabilité est S3 Object Lock.
Elle permet de stocker un objet (ici un fichier JSON / un blob contenant la racine + une signature
ED25519) avec deux garanties :
L’objet ne peut pas être modifié ni supprimé tant que la période de rétention n’est pas écoulée (Write Once Read Many)
Toute tentative de remplacement crée une nouvelle version ; on peut aussi appliquer un legal hold pour bloquer la suppression administrative.
En pratique, cela signifie qu’un simple upload suffit à rendre le checkpoint inaltérable jusqu’à la période de rétention choisie.
aws s3api put-object \
--bucket merkle-checkpoints \
--key roots/2025-10-01.json \
--object-lock-mode COMPLIANCE \
--object-lock-retain-until-date 2025-12-31T00:00:00Z \
--body checkpoint.json
Exemple d’object locking avec le CLI AWS
L’application ne gère plus l’immutabilité, elle est déléguée au Cloud Provider (ici AWS).
Alternatives chez d’autres fournisseurs
Azure Blob Storage : propose immutable blob policies et legal holds, avec des mécanismes similaires (durée de rétention ou verrou juridique).
Google Cloud Storage : offre les Object Retention Policies et Bucket Lock, verrouillant les objets sur des durées prédéfinies.
MinIO : en self-hosted, implémente aussi Object Lock, compatible avec l’API S3 (fiable à condition d’avoir une infrastructure zero trust).
Pourquoi cette approche est idéale
Elle répond directement aux exigences de rétention des normes comme NF525, PCI-DSS ou HDS : le checkpoint est en mode Write Once, Read Many (WORM). Si des logs bruts étaient effacés ailleurs, la preuve d’inclusion échouerait, rendant la suppression détectable ; pour la prévention, on stocke aussi les logs dans un bucket avec rétention/Object Lock.
Chaque checkpoint est un objet de quelques octets stocké une seule fois, le coût est donc négligeable par rapport au volume des logs eux-mêmes.
Une racine par jour / semaine suffit ; elles peuvent être répliquées et signées pour renforcer la traçabilité.
Optimisation des coûts et design opérationnel
L’objectif n’est pas seulement d’être conforme, mais de rester efficace en stockage et en calculs.
Stockage
Le volume de logs croît souvent très rapidement, une bonne pratique consiste à dissocier les preuves Merkle des logs :
Compute
Grâce à la structure Merkle, la vérification d’un log donné est logarithmique. Même si l’historique complet contient plusieurs millions d’événements, l’intégralité n’est jamais nécessaire, ce qui permet d’économiser en egress.
Conclusion
Ce proof of concept montre qu’il est possible de garantir l’intégrité d’un journal de logs sans chaîne de hachage, sans base de données spécialisée, et sans infrastructure complexe.
En combinant des primitives simples (SHA-256 / BLAKE3, Merkle tree, stockage immuable) et des mécanismes cloud natifs comme S3 Object Lock, on obtient un système vérifiable, frugal et conforme aux exigences de traçabilité modernes.
Cette solution ne remplace pas la gouvernance ou la supervision applicative, mais est une base cryptographique solide sur laquelle construire un audit trail durable et transparent.

















_ZRNfyf.webp)
